Minimale Mannhattan-Netzwerke

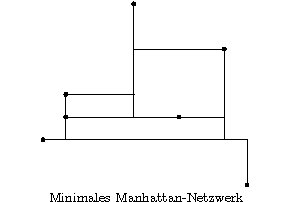
Ein Manhattan-Netzwerk für eine Menge von n Punkten in der Ebene ist die Vereinigung von vertikalen und horizontalen Strecken, so dass jedes Punktepaar durch einen kürzesten Treppenstufenweg, einen Manhattan-Weg, verbunden ist. Ein Netzwerk, das unter allen Manhattan-Netzwerken minimale Gesamtlänge hat, heisst minimales Manhattan-Netzwerk. Der Komplexitätsstatus des Problems ist nach wie vor offen.

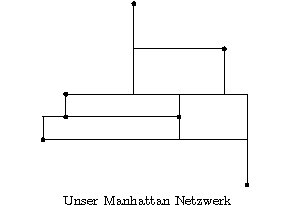
Es ist uns gelungen einen Algorithmus zu entwerfen, der eine 3-Approximation eines Manhattan-Netzwerks, also ein Manhattan-Netzwerk das höchstens dreimal so lang ist wie ein minimales, in O(n log n) Zeit berechnet. Links ist ein minimales Manhatten-Netzwerk abgebildet dessen Länge 36 ist. Rechts sieht man die Ausgabe unseres Algorithms, die Länge ist 41. Unser Algorithmus kann hier getestet werden. Zur praktischen Evaluierung unseres Algorithmus haben wir das Problem als gemischt ganzzahliges Problem modelliert und mit einem dementsprechenden Solver gelöst. Dabei hat sich herausgestellt, dass unser Algorithmus in der Praxis weit bessere Lösungen liefert als dies der Faktor von 3 vermuten läßt, eine genaue Analyse läßt sich [1] entnehmen. Im Schnitt waren unsere Manhattan-Netzwerke nur 1,3 mal länger als die dementsprechenden minimalen.

In der Zwischenzeit ist es einer Gruppe französischer Forscher gelungen, einen 2-approximativen Algorithmus für das Problem anzugeben. Sie runden dafür die Lösungsvariablen der Relaxierung des gemischt ganzzahligen Programms.

In Zusammenarbeit mit Takeshi Shirabe und Florian Widmann.

1. Marc Benkert, Alexander Wolff, Florian Widmann, and Takeshi Shirabe. The minimum Manhattan network problem: Approximations and exact solutions. Computational Geometry: Theory and Applications, 35(3):188-208, 2006. [ bib | html | pdf | abstract ]
2. Marc Benkert, Florian Widmann, and Alexander Wolff. The minimum Manhattan network problem: A fast factor-3 approximation. In Jin Akiyama, Mikio Kano, and Xuehou Tan, editors, Proc. 8th Japanese Conf. on Discrete and Computational Geometry (JCDCG'04), volume 3742 of Lecture Notes in Computer Science, pages 16-28. Springer-Verlag, 2005. [ bib | html | pdf ]
3. Marc Benkert, Florian Widmann, and Alexander Wolff. The minimum Manhattan network problem: A fast factor-3 approximation. Technical Report 2004-16, Fakultät für Informatik, Universität Karlsruhe, 2004. Available at http://digbib.ubka.uni-karlsruhe.de/volltexte/1000003164. [ bib | html | pdf ]
4. Alexander Wolff, Marc Benkert, and Takeshi Shirabe. The minimum Manhattan network problem: Approximations and exact solutions. In Proc. 20th European Workshop on Computational Geometry (EWCG'04), pages 209-212, Sevilla, 2004. [ bib | pdf ]