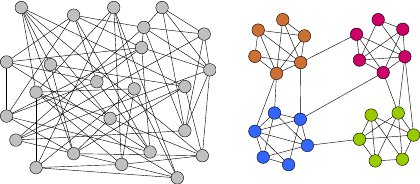
Gegenstand vieler meiner Forschungsarbeiten ist das Auffinden und Quantifizieren von Clusterstruktur in Netzwerken. Das Bild zeigt zweimal dasselbe Netzwerk, links als unsortierter Haufen, rechts mit aufgezeigter Clusterstruktur. Praktische relevante Instanzen reichen bis zu einer Größe von mehreren Millionen oder sogar Milliarden Elementen. Beispielthemen:

• Qualitätsmaße und Kriterien für Clusterungen sowie deren Verhalten und Eigenschaften
• Algorithmische Komplexität von Kriterien, Berechenbarkeit, Optimierung, Approximation
• Algorithmische Herangehensweisen beim Graphenclustern, Heuristiken

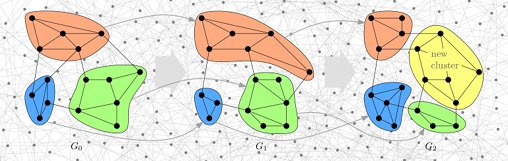
Typischerweise sind Netzwerke Änderungen unterworfen, welche sich in den Clustern niederschlagen (oder sogar durch sie motiviert sind?). Das Bild zeigt drei Zeitschritte eines Netzwerks, und seiner sich verändernden Clusterstruktur. Beispielthemen:

• Problemstellung 1: Online-Update der Clusterung nach Änderng im Netzwerk: schnell, reibungslos und gut, i.e., geringe Laufzeit, glatte/stetige Übergänge der Clusterung bei einem Update, geringe Qualitätseinbußen gegenüber einem statischen Verfahren (tatsächlich ist es möglich in allen drei Kriterien besser zu sein).
• Problemstellung 2: Zeitliche Sequenz (offline) eines veränderlichen Graphen ist gegeben, Untersuchung der zeitlichen Entwicklung der Clusterstruktur des Graphen, Finden von Umbrüchen in der Clusterung, Verfolgen von sich wandelnden Clustern über die Zeit

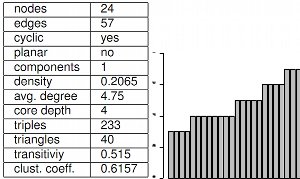
Eine Vielzahl von Maßzahlen und Eigenschaften existieren um ein Netzwerk, oder Teile davon, zu beschreiben, und deren Rolle und Relevanz zu analysieren. Das Bild zeigt einen Auszug solcher Zahlen und die Gradverteilung für den Graphen ganz oben. Im weiteren Sinne gehört zu diesem Thema auch die Simulation und die Modellierung eines Netzwerks. Beispielthemen:

• Mathematische Modellierung von Problemen auf Netzwerken
• Eigenschaften von Netzwerken, z.B. k-Core Dekomposition, Zentralitätsmaße, Verteilungen
• Erzeugung künstlicher Zufallsnetzwerke: Effizienz, Vollständigkeit, unter Einhaltung gewisser erwünschter Eigenschaften, beispielsweise G(n,pin,pout), k-core, preferential attachment

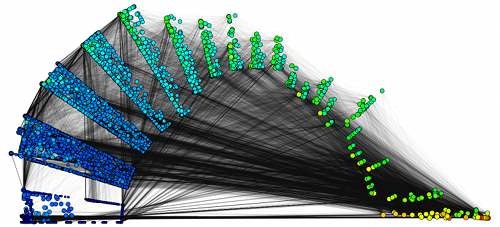
Visualisierung sind der Schlüssel zur explorativen Netzwerkanalyse, mehrere Eigenschaften gleichzeitig können im Kontext des Netzwerks dargestellt werden. Das Bild zeigt das Netzwerk der autonomen Systeme im Internet, Kuchenstücke entsprechen der Core-Zerlegung, Farbe dem Knotengrad und Fläche der Knotenzentralität. Das Layout richtet sich nach Verbindungen (LunarVis). Beispielthemen:

• Analytische Visualisierungen und Netzwerk-Fingerabdrücke
• Analyse der Core-Hierarchie des AS-Netzwerks und von P2P-Netzwerken
• Visualisierung von Protein-Protein Ähnlichkeiten bei Medikation

Meine Forschung orientiert sich stets sowohl an theoretischen Zielsetzungen als auch an praktischer Sinnhaftigkeit. Dabei nutze ich Daten aus verschiedenen Anwendungen, eine Auswahl sind:

• Anonymisierte Bondaten aus Einkäufen
• Reaktion von Proteinen bei Behandlungen
• Netzwerk der Autotnomen Systeme im Internet
• Straßennetzwerke und Netzwerke aus öffentlichen Verkehrsmitteln
• Kollaborations- und Zitationsnetzwerke
• Virtuelle soziale Netzwerke

• ILP-Modellierung kombinatorischer Probleme
• Datenstrukturen und Algorithm Engineering, insbesondere beim Graphenclustern
• Flüsse, Schnitte, Matroide, Planarität, Layoutprobleme, Springembedder
• Voronoi Diagramme