im Rahmen der FYS „Dynamisierung multiterminaler Flüsse in Form von Gomory-Hu-Bäumen“

Dr. Tanja Hartmann

• Kenntnisse im Bereich der Algorithmentechnik
• Interesse an graphentheoretischen Fragestellungen
• Je nach Tätigkeit, Kenntnisse in C++ und/oder Java

Im Rahmen untenstehender Themenstellung sind ab April 2010 mehrere Hiwi-Stellen sowohl im Bereich der Implementierung und Durchführung von Experimenten als auch im Bereich der theoretischen Analyse zu vergeben. Interessenten wenden sich bitte an Dr. Tanja Hartmann.

Bei der Dynamisierung multiterminaler Flüsse geht es um die Entwicklung eines algorithmischen Ansatzes zur dynamischen Aktualisierung von Gomory-Hu-Bäumen und um die experimentelle Untersuchung des Verhaltens dieses Algorithmus bezüglich verschiedener Klassen von Graphen.

Das multiterminale Flussproblem fragt nach allen paarweisen, minimalen s-t-Schnitten eines Graphen. Ein minimaler s-t-Schnitt teilt einen Graphen so in zwei disjunkte Teilgraphen, dass die Quelle s in einem Teilgraph, die Senke t im anderen Teilgraph liegt, und dass die Summe der Kantengewichte, die vom s-Teilgraphen in den t-Teilgraphen reichen, minimal wird über alle Schnitte dieser Art.

Der von Gomory und Hu [GH61] vorgestellte Gomory-Hu-Baum zur Repräsentation aller paarweisen, minimalen s-t-Schnitte ist wie folgt definiert:

Ein Gomory-Hu-Baum zu einem gegebenen ungerichteten, gewichteten Graphen G, ist ein gewichteter, spannender Baum, in dem jede Kante einen minimalen s-t-Schnitt bezüglich der beiden inzidenten Knoten repräsentiert. Das heißt, entnimmt man die Kante, so zerfällt der Baum in die beiden Schnitt-Teilgraphen, das Gewicht der Kante entspricht dem Schnittgewicht.

Als Konsequenz dieser Eigenschaft ist der minimale s-t-Schnitt bezüglich zweier im Baum nicht adjazenten Knoten s und t durch eine minimal gewichtete Kante auf dem eindeutigen Pfad zwischen s und t gegeben. Insbesondere repräsentiert jeder Gomory-Hu-Baum eine minimale Schnittbasis. Die Kantenmenge eines Gomory-Hu-Baums muss dabei keine Kantenteilmenge des zugrundeliegenden Graphen sein.

Die von Gomory und Hu entwickelte iterative Methode zur Konstruktion solcher Bäume beginnt mit einem Superknoten, der alle Knoten des Graphen beinhaltet. In n-1 Iterationsschritten werden dann minimale s-t-Schnitte (maximale s-t-Flüsse) berechnet. In jedem Schritt wird einer der noch bestehenden Superknoten mit Hilfe des berechneten Schnitts in zwei neue nichtleere Superknoten geteilt und zu einer Baumstruktur aus Superknoten verbunden, solange, bis nur noch einelementige Superknoten bestehen. Dieses Vorgehen ist unabhängig vom verwendeten Flow-Algorithmus zur Berechnung der minimalen s-t-Schnitte.

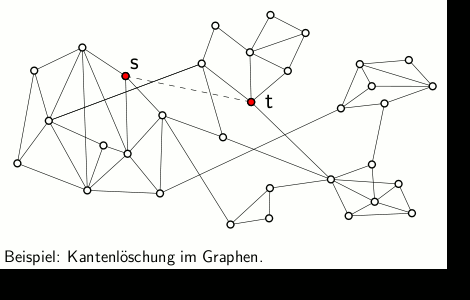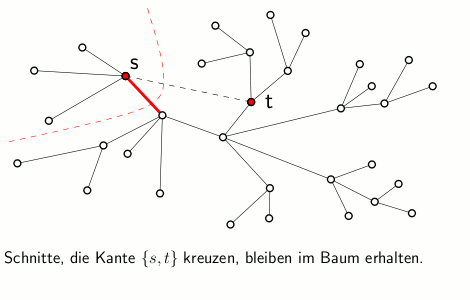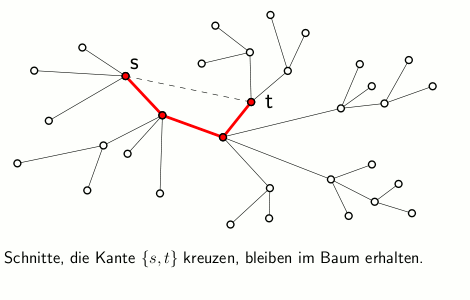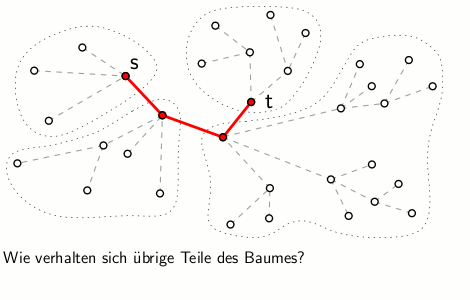Eine Dynamisierung der Gomory-Hu-Baumkonstruktion soll nun folgendes leisten: Betrachtet man zum Beispiel den Fall einer Kantenlöschung im zugrundeliegenden Graphen, so sieht man leicht ein, dass im vorherigen Gomory-Hu-Baum genau die Kanten weiterhin minimale s-t-Schnitte repräsentieren, die auf dem Pfad zwischen den beiden Knoten liegen, deren Kante im Graph gelöscht wurde. Für alle übrigen Knotenpaare (die keine Pfadkante definieren) gilt es, eine gute und schnelle Aktualisierung der zugehörigen minimalen s-t-Schnitte zu finden und diese gemeinsam mit den bestehenden Pfadkanten wieder in einer entsprechenden Baumstruktur zu repräsentieren.

Das Hauptproblem hierbei sind die globalen Auswirkungen einer Kantenänderung auf die minimalen s-t-Schnitte. Interessant ist daher auch die Frage nach der Existenz bestimmter Graphklassen, deren charakteristische Eigenschaften eine gewisse lokale Beschränktheit der Änderung garantieren. Für solche Graphen lassen sich eventuell spezielle Ansätze entwickeln, die genau diese Lokalität im klassischen Sinne der Dynamisierung ausnutzen. Die Unabhängigkeit der Gomory-Hu-Methode von den Details der eigentlichen s-t-Schnittberechnung wirft außerdem die Frage auf, inwieweit sich durch eine Dynamisierung der einzelnen Flussberechnung ein Vorteil für die dynamische Aktualisierung ganzer Gomory-Hu-Bäume erzielen lässt.

• [GH61]
  R. E. Gomory and T.C. Hu. Multi-Terminal Network Flows. Journal of the Society for Industrial and Applied Mathematics, 9:551–570, December 1961.