Minimum Mannhattan Networks

Given a set of n points in the plane, a Manhattan network is the union of vertical and horizontal line segments. such that each pair of points is connected by a shortest rectilinear staircase path, a Manhattan path. We call a network a minimum Manhattan network if the total length of its segments is minimum among all Manhattan networks. The complexity status of the problem is still unknown.

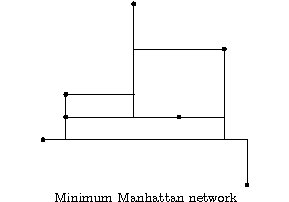
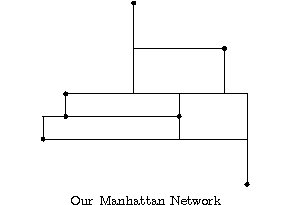
We established a factor-3 approximation algorithm that runs in O(n log n) time. On the left hand you see an example of a minimum Manhattan network, its length is 36. On the right hand you see the Manhattan network computed by our algorithm is depicted, its length is 41. You can test the algorithm here . Furthermore, we implemented a mixed integer program to solve the problem optimally in order to measure the practical results of our algorithm. The results of our practical evaluation can be seen in [1]. It turned out that our algorithm performs better in practice than the theoretic factor of 3 suggests. On average our Manhattan networks were only 1.3 times longer than the corresponding minimum ones.

In the meantime a group of French researchers managed to come up with a factor-2 approximation algorithm. Their algorithm is based on a technique that rounds the solution variables of the relaxed mixed inter program.

Joint work with Takeshi Shirabe and Florian Widmann.