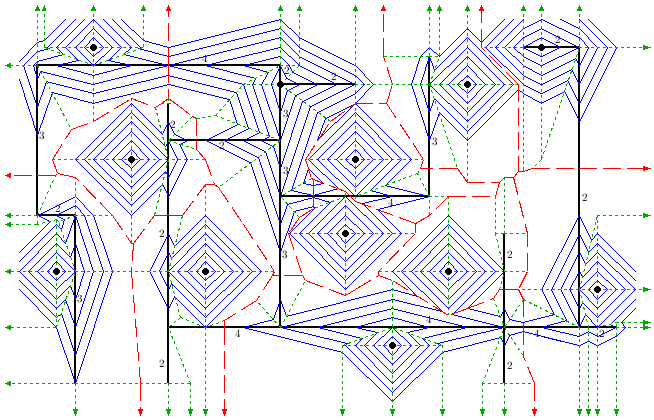
Voronoi-Diagramm für die City-Metrik

Gegeben sei eine Menge S von n Punkten in der Ebene. Unter Verwendung der City-Metrik partitioniert das City Voronoi Diagramm die Ebene in die Voronoi-Regionen der Punkte. Diese Metrik wird durch schnellste Pfade induziert, welche bezüglich der Manhattan-Metrik und einem beschleunigenden Transportnetzwerk gemessen werden. Das Transportnetzwerk besteht aus c disjunkten achsenparallelen Strecken. Wir beschreiben einen Algorithmus, der das City Voronoi Diagramm (einschließlich der Informationen über schnellste Pfade) unter Verwendung einer Wellenfrontausdehnung in einer asymptotischen Laufzeit von O( (c + n) polylog(c + n) ) erstellt. Das Motiv zeigt ein City-Voronoi-Diagramm und einen Teil einer Wellenfrontausdehnung.

Robert Görke gewann auf dem zweiten internationalen Symposium on Voronoi Diagrams in Science and Engineering (VD'05) am 13. Oktober 2005 den Preis für die „Beste Präsentation eines jungen Vortragenden“ [1].

Auf derselben Konferenz gewann er den Wettbewerb um das beste Motiv für den Einband des Tagungsbandes.

1. Robert Görke, Chan-Su Shin, and Alexander Wolff. Constructing the city Voronoi diagram faster. International Journal of Computational Geometry and Applications, 18(4), 2008. To appear. [ bib | pdf | abstract ]
2. Robert Görke and Alexander Wolff. Constructing the city Voronoi diagram faster. In Proc. 2nd Internat. Symp. on Voronoi Diagrams in Science and Engineering (VD'05), pages 162-172, Seoul, 2005. [ bib | pdf ]
3. Robert Görke and Alexander Wolff. Constructing the city Voronoi diagram faster. In Proc. 21st European Workshop on Computational Geometry (EWCG'05), pages 155-158, Eindhoven, 2005. [ bib | pdf ]
4. Robert Görke. Ein schneller Konstruktionsalgorithmus für eine Quickest-Path-Map bezüglich der City-Metrik. Master's thesis, Fakultät für Informatik, Universität Karlsruhe, September 2004. [ bib | pdf ]