Verification of Shortest-Path Algorithms
Diploma/Master Thesis
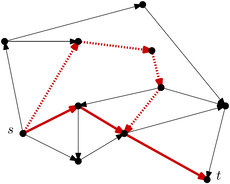
[ ] Route planning in transportation networks is one of the most active topics in the research field of Algorithm Engineering with many real world applications like navigation systems, online route planning systems (e.g. Google Maps) or timetable information systems. Usually, the transportation network is modeled as a weighted graph. Then, the problem can be solved by applying Dijkstra's algorithm to find the shortest-path between two nodes s and t. In recent years, many so-called speed-up techniques have been developed for Dijkstra's algorithm that accelerate query times by a factor of up to 3 Million.
] Route planning in transportation networks is one of the most active topics in the research field of Algorithm Engineering with many real world applications like navigation systems, online route planning systems (e.g. Google Maps) or timetable information systems. Usually, the transportation network is modeled as a weighted graph. Then, the problem can be solved by applying Dijkstra's algorithm to find the shortest-path between two nodes s and t. In recent years, many so-called speed-up techniques have been developed for Dijkstra's algorithm that accelerate query times by a factor of up to 3 Million.
In order to get the best results, implementations of these algorithms are highly optimized. Thus, there is a high chance that the code contains bugs that are not discovered by manual testing. Such bugs can lead to wrong results or—even worse—may cause the program to crash.
In recent years, various systematic testing techniques have been developed that automatically check the code for deep, complex bugs. In this project, we will investigate how to apply such techniques to the implementations of shortest path algorithms. We will start with one of the state-of-the-art approaches, and improve it by developing different domain-specific optimizations until it can handle our shortest path code with a reasonable performance.
Goals
- Implement shortest-path algorithms in Java.
- Express the shortest path problem in a relational first order logic efficiently.
- Optimize an existing program checking technique until it handles the shortest path code.
Requirements
- Established knowledge in algorithmics and formal verification.
- Familiarity with first order logic.
- Knownledge in Java and C++ is helpful but not mandatory.
Contact
Notes
- Available from January 2010 on.
- The thesis will be supervised and written in English language.