Boundary Labeling
How to produce easy-to-understand labelings?
Boundary labelings are applied, e.g., in order to label places or regions in geographic maps if the direct placement of the labels inside the illustration is impossible or overly reduces legibility. In this case the labels are placed aside the illustration and points and labels are connected by arcs. This yields a labeling problem that also includes graph drawing problems:
Given are n points in a rectangle R and an equal number of uniform rectangular labels at the left and/or right boundary of R. The aim is to connect points and labels by arcs (also denoted as leaders) such that the illustration is easy to read for human viewers. Therefore, leaders must not intersect and have a uniform look: they consist of a horizontal segments and potentially a vertical (or diagonal) segment.
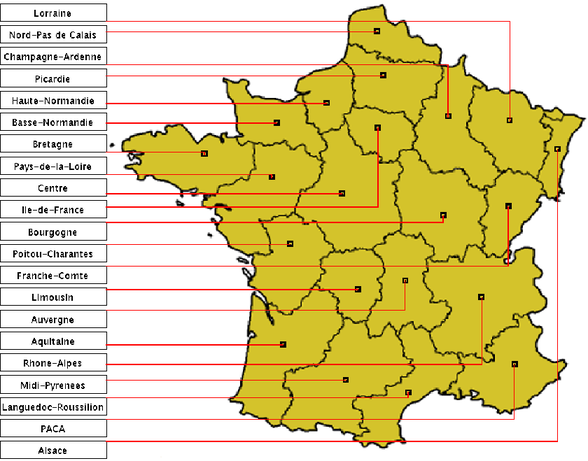
The figure below shows a labeling of the regions of France as computed by our algorithm. The number of bends as well as the length of all leaders are minimized.
The algorithm has been implemented as a Java applet that can be tested with any background image.
Joint work with a) Michael Bekos, Michael Kaufmann and Antonios Symnvonis and with b) Herman Haverkort and Moritz Kroll.
Publications
- Michael A. Bekos, Michael Kaufmann, Martin Nöllenburg, and Antonios Symvonis. Boundary labeling with octilinear leaders. In Proc. 11th Scandinavian Workshop on Algorithm Theory (SWAT'08), 2008. To appear. [ bib ]
- Marc Benkert, Herman Haverkort, Moritz Kroll, and Martin Nöllenburg. Algorithms for multi-criteria one-sided boundary labeling. In Proc. 15th Int. Symp. Graph Drawing (GD '07), 2007. To appear. [ bib ]
- Marc Benkert and Martin Nöllenburg. Improved algorithms for length-minimal one-sided boundary labeling. In Proc. 23rd European Workshop on Computational Geometry (EWCG'07), pages 190-193, Graz, Austria, 2007. [ bib | pdf ]
- Michael A. Bekos, Michael Kaufmann, Antonios Symvonis, and Alexander Wolff. Boundary labeling: Models and efficient algorithms for rectangular maps. Computational Geometry: Theory and Applications, 36(3):215-236, 2007. [ bib | html | pdf | abstract ]
- Michael A. Bekos, Michael Kaufmann, Antonios Symvonis, and Alexander Wolff. Boundary labeling: Models and efficient algorithms for rectangular maps. In János Pach, editor, Proc. 12th Internat. Sympos. Graph Drawing (GD'04), volume 3383 of Lecture Notes in Computer Science, pages 49-59. Springer-Verlag, 2005. [ bib | html | pdf | abstract ]